题目描述

我们定义了一个函数 countUniqueChars(s) 来统计字符串 s 中的唯一字符，并返回唯一字符的个数。

例如：s = "LEETCODE" ，则其中 "L", "T","C","O","D" 都是唯一字符，因为它们只出现一次，所以 countUniqueChars(s) = 5 。

本题将会给你一个字符串 s ，我们需要返回 countUniqueChars(t) 的总和，其中 t 是 s 的子字符串。输入用例保证返回值为 32 位整数。

注意，某些子字符串可能是重复的，但你统计时也必须算上这些重复的子字符串（也就是说，你必须统计 s 的所有子字符串中的唯一字符）。

示例 1：

1
2
3
4
5
输入: s = "ABC"
输出: 10
解释: 所有可能的子串为："A","B","C","AB","BC" 和 "ABC"。
     其中，每一个子串都由独特字符构成。
     所以其长度总和为：1 + 1 + 1 + 2 + 2 + 3 = 10

示例 2：

1
2
3
输入: s = "ABA"
输出: 8
解释: 除了 countUniqueChars("ABA") = 1 之外，其余与示例 1 相同。

示例 3：

1
2
输入：s = "LEETCODE"
输出：92

提示：

  • 1 <= s.length <= 10^5
  • s 只包含大写英文字符

来源：力扣（LeetCode）

题解

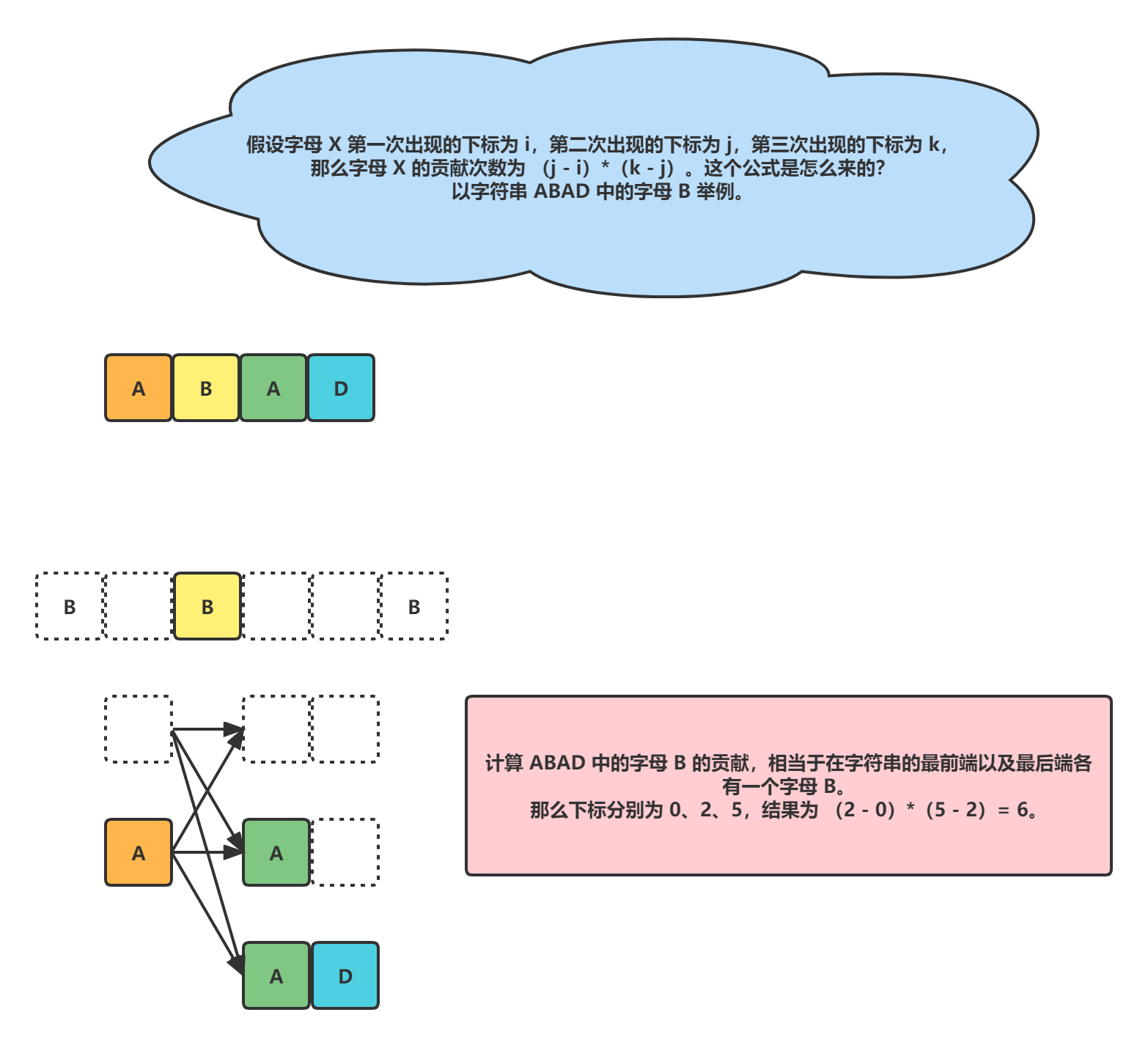
CountUniqueCharactersOfAllSubstringsOfAGivenString

以字符串 "ABA" 为例，第一个字母 A 符合条件的子字符串为 "A"，"AB"；第二个字母 A 符合条件的子字符串为 "BA"，"A"；字母 B 符合条件的子字符串为 "B"，"AB"，"BA"，"ABA"，总计：2 + 2 + 4 = 8。

哈希表

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
public int uniqueLetterString(String s) {
    Map<Character, List<Integer>> indexMap = new HashMap<>();
    for (int i = 0; i < s.length(); i++) {
        char c = s.charAt(i);
        if (!indexMap.containsKey(c)) {
            indexMap.put(c, new ArrayList<Integer>());
            indexMap.get(c).add(-1);
        }
        indexMap.get(c).add(i);
    }

    int ans = 0;
    for (Character character : indexMap.keySet()) {
        List<Integer> indexList = indexMap.get(character);
        indexList.add(s.length());
        // 如果字母存在于 HashMap 中, 那么出现次数必定不小于 1. 而且放了两个哨兵, 所以不用考虑边界.
        for (int i = 1; i < indexList.size() - 1; i++) {
            ans += (indexList.get(i) - indexList.get(i - 1)) * (indexList.get(i + 1) - indexList.get(i));
        }
    }

    return ans;
}
  • 时间复杂度： O(n)
  • 空间复杂度： O(n)

submissions-2022090602

数组

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
public int uniqueLetterString(String s) {
    int n = s.length();

    // 存储字母两次出现的位置
    int[][] arr = new int[26][2];
    for (int i = 0; i < 26; i++) {
        arr[i] = new int[] {-1, -1};
    }

    int ans = 0;
    for (int i = 0; i < n; i++) {
        // 字母第一次出现的位置默认为 -1，也就是说字母出现第 2 次的时候就可以进行计算
        int idx = s.charAt(i) - 'A';
        if (arr[idx][1] != -1) {
            ans += (arr[idx][1] - arr[idx][0]) * (i - arr[idx][1]);
            arr[idx][0] = arr[idx][1];
        }
        arr[idx][1] = i;
    }

    // 处理没有处理到的数据
    for (int i = 0; i < 26; i++) {
        if (arr[i][1] != -1) {
            ans += (arr[i][1] - arr[i][0]) * (n - arr[i][1]);
        }
    }

    return ans;
}
  • 时间复杂度： O(n)
  • 空间复杂度： O(n)

submissions-2022090601

参考资料

__END__