题目描述

给你两个整数 n 和 k ，请你构造一个答案列表 answer ，该列表应当包含从 1 到 n 的 n 个不同正整数，并同时满足下述条件：

  • 假设该列表是 answer = [a1, a2, a3, ... , an] ，那么列表 [|a1 - a2|, |a2 - a3|, |a3 - a4|, ... , |an-1 - an|] 中应该有且仅有 k 个不同整数。

返回列表 answer 。如果存在多种答案，只需返回其中 任意一种 。

示例 1：

1
2
3
输入：n = 3, k = 1
输出：[1, 2, 3]
解释：[1, 2, 3] 包含 3 个范围在 1-3 的不同整数，并且 [1, 1] 中有且仅有 1 个不同整数：1

示例 2：

1
2
3
输入：n = 3, k = 2
输出：[1, 3, 2]
解释：[1, 3, 2] 包含 3 个范围在 1-3 的不同整数，并且 [2, 1] 中有且仅有 2 个不同整数：1 和 2

提示：

1 <= k < n <= 10^4

来源：力扣（LeetCode）

题解

找规律

BeautifulArrangementII

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
public int[] constructArray(int n, int k) {
    int[] ans = new int[n];
    int ascNum = 1;
    int descNum = n;
    // 先处理前 k 个数字
    // 当下标为偶数的时候, 是按照升序排列, 从数字 1 开始
    // 当下标为奇数的时候, 是按照降序排列, 从数字 n 开始
    for (int i = 0; i < k; i++) {
        if (i % 2 == 0) ans[i] = ascNum++;
        else ans[i] = descNum--;
    }

    // 处理剩余 n - k 个数字, 不难看出剩余的数字要么按照下标 k - 1 位置数字升序排列, 要么降序排列
    // 当 k 为奇数的时候, 升序排列
    // 当 k 为偶数的时候, 降序排列
    if (k % 2 == 1) {
        for (int i = k; i < n; i++) ans[i] = ascNum++;
    } else {
        for (int i = k; i < n; i++) ans[i] = descNum--;
    }
    return ans;
}
  • 时间复杂度： O(n)
  • 空间复杂度： O(n)

submissions-2022090801

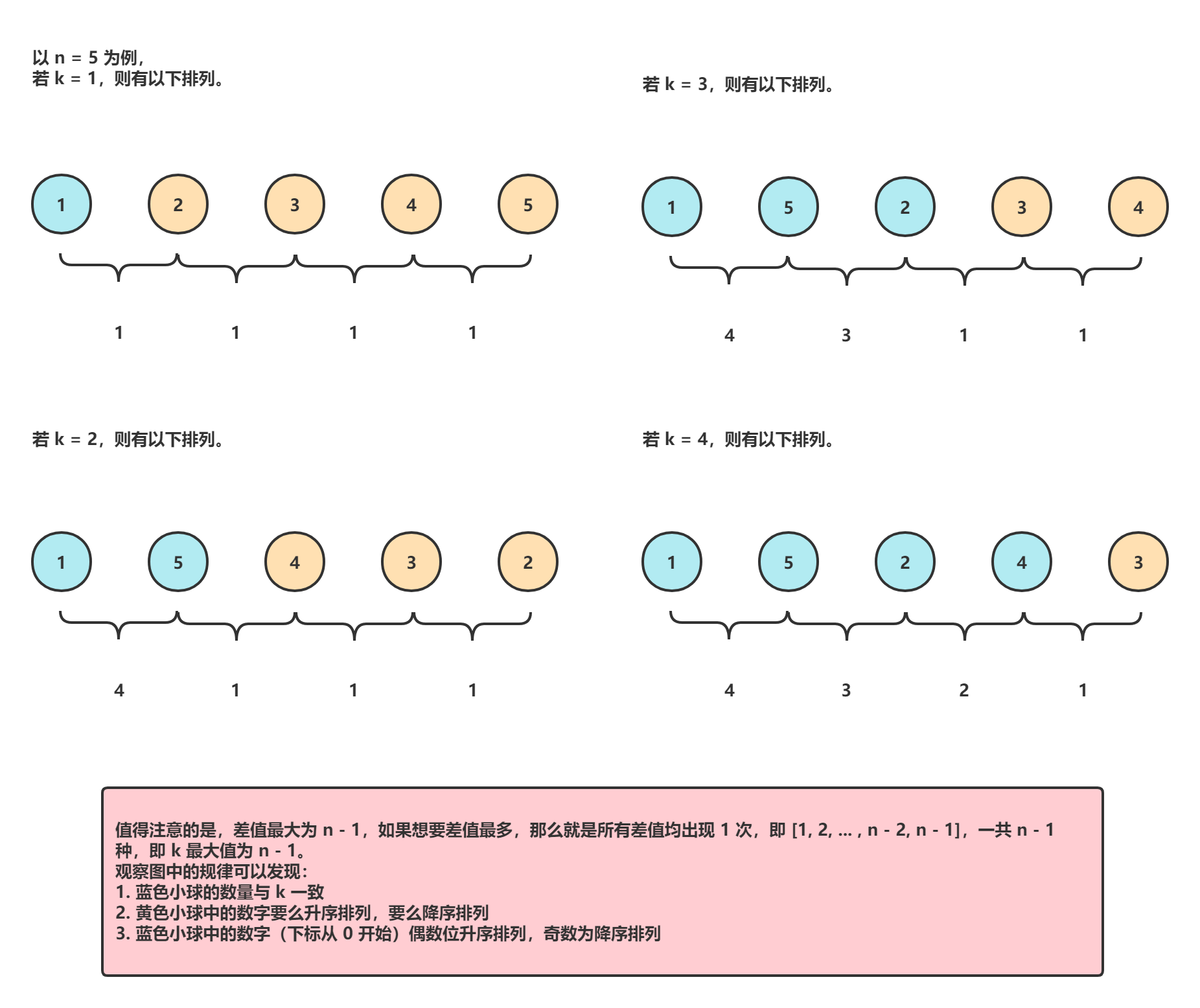
构造

给定范围在 [1, n] 的 n 个数，当 直接升序/降序 排列时，相邻项差值为 1，仅一种；而从 首位 开始按照 升序 间隔排列，次位 开始按照 降序 间隔排列（即排列为 [1, n, 2, n - 1, 3, ...]）时，相邻差值会从 n - 1 开始递减至 1，共 n - 1 种。

那么当我们需要构造 k 种序列时，我们可以先通过 直接升序 的方式构造出若干个 1，然后再通过 间隔位分别升降序 的方式构造出从 k 到 1 的差值，共 k 个。

显然，我们需要 k + 1 个数来构造出 k 个差值。因此我们可以先从 1 开始，使用 n - (k + 1) 个数来 直接升序（通过方式一构造出若干个 1），然后从 n - k 开始间隔升序排列，按照 n 开始间隔降序排列，构造出剩下的序列。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
public int[] constructArray(int n, int k){
    int[] ans = new int[n];
    // 需要使用 k + 1 个数字构造差值为 [1, k] 的 k 种序列
    // 所以, 剩余 n - (k + 1) 个数字为升序排列
    int ascCount = n - (k + 1);
    for (int i = 0; i < ascCount; i++) ans[i] = i + 1;

    // 间隔升序以及间隔降序 差值为 k, 最大数字为 n, 那么另外的数字必定为 n - k, 且 n - k < n
    for (int i = ascCount, ascNum = n - k, descNum = n; i < n; ) {
        ans[i++] = ascNum++;
        // 当 i = n - 1 时, 处理完升序的数据, 此时经过 i++, i 大小已经变成了 n, 所以必须添加判断
        if (i < n) ans[i++] = descNum--;
    }
    return ans;
}
  • 时间复杂度： O(n)
  • 空间复杂度： O(n)

submissions-2022090802

参考资料

__END__