题目描述

整数数组 nums 按升序排列，数组中的值 互不相同 。

在传递给函数之前，nums 在预先未知的某个下标 k（0 <= k < nums.length）上进行了 旋转，使数组变为 [nums[k], nums[k+1], ..., nums[n-1], nums[0], nums[1], ..., nums[k-1]]（下标 从 0 开始 计数）。例如， [0,1,2,4,5,6,7] 在下标 3 处经旋转后可能变为 [4,5,6,7,0,1,2] 。

给你 旋转后 的数组 nums 和一个整数 target ，如果 nums 中存在这个目标值 target ，则返回它的下标，否则返回 -1 。

你必须设计一个时间复杂度为 O(log n) 的算法解决此问题。

示例 1：

1
2
输入：nums = [4,5,6,7,0,1,2], target = 0
输出：4

示例 2：

1
2
输入：nums = [4,5,6,7,0,1,2], target = 3
输出：-1

示例 3：

1
2
输入：nums = [1], target = 0
输出：-1

提示：

  • 1 <= nums.length <= 5000
  • -10^4 <= nums[i] <= 10^4
  • nums 中的每个值都 独一无二
  • 题目数据保证 nums 在预先未知的某个下标上进行了旋转
  • -10^4 <= target <= 10^4

来源：力扣（LeetCode）

题解

二分查找

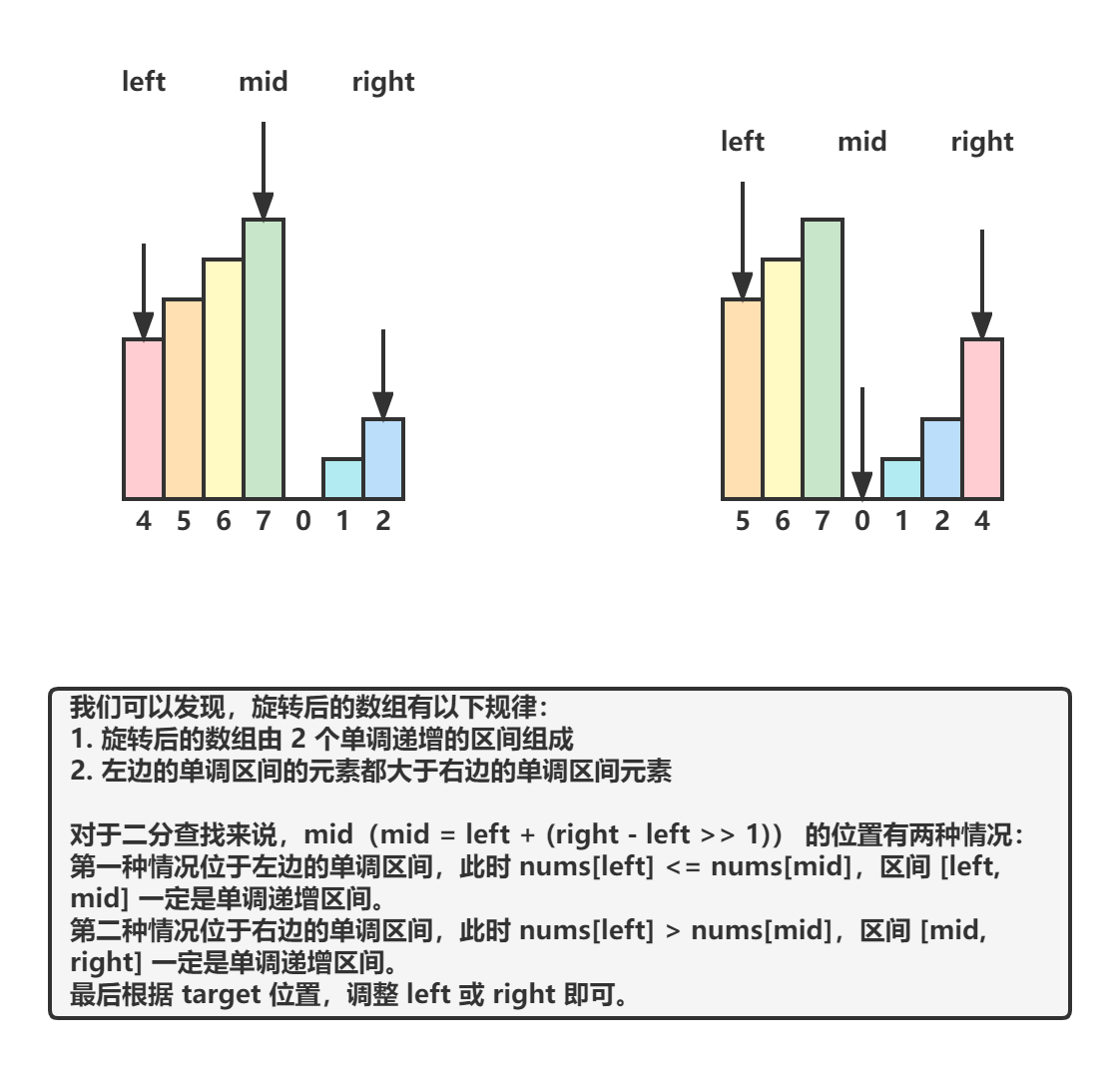
对于有序数组，可以使用二分查找的方法查找元素。

但是这道题中，数组本身不是有序的，进行旋转后只保证了数组的局部是有序的，这还能进行二分查找吗？答案是可以的。

SearchInRotatedSortedArray

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
public int search(int[] nums, int target) {
    int left = 0;
    int right = nums.length - 1;
    while (left <= right) {
        int mid = left + (right - left >> 1);
        if (nums[mid] == target) return mid;
        // 因为 int mid = left + (right - left >> 1), 所以当 left = right - 1 的时候, mid = left.
        // 由于这个数组不是一定满足单调递增, 所以没办法确定 left 与 right 位置元素的大小关系, 所以要将 nums[mid] == nums[left] 包含在内.
        // 所以这里必须是 nums[left] <= nums[mid].
        // 如果 int mid = left + (right - left + 1 >> 1), 则对应 nums[left] < nums[mid].
        if (nums[left] <= nums[mid]) {
            // 区间 [left, mid] 属于单调递增区间
            if (nums[left] <= target && target < nums[mid]) {
                right = mid - 1;
            } else {
                left = mid + 1;
            }
        } else {
            // 区间 [mid, right] 属于单调递增区间
            if (nums[mid] < target && target <= nums[right]) {
                left = mid + 1;
            } else {
                right = mid - 1;
            }
        }
    }
    return -1;
}
  • 时间复杂度： O(logn)
  • 空间复杂度： O(1)

submissions-2022090901

参考资料

__END__