题目描述

给你一个非负整数数组 nums 。如果存在一个数 x ，使得 nums 中恰好有 x 个元素 大于或者等于 x ，那么就称 nums 是一个 特殊数组 ，而 x 是该数组的 特征值 。

注意： x 不必 是 nums 的中的元素。

如果数组 nums 是一个 特殊数组 ，请返回它的特征值 x 。否则，返回 -1 。可以证明的是，如果 nums 是特殊数组，那么其特征值 x 是 唯一的 。

示例 1：

1
2
3
输入：nums = [3,5]
输出：2
解释：有 2 个元素（3 和 5）大于或等于 2 。

示例 2：

1
2
3
4
5
6
7
输入：nums = [0,0]
输出：-1
解释：没有满足题目要求的特殊数组，故而也不存在特征值 x 。
如果 x = 0，应该有 0 个元素 >= x，但实际有 2 个。
如果 x = 1，应该有 1 个元素 >= x，但实际有 0 个。
如果 x = 2，应该有 2 个元素 >= x，但实际有 0 个。
x 不能取更大的值，因为 nums 中只有两个元素。

示例 3：

1
2
3
输入：nums = [0,4,3,0,4]
输出：3
解释：有 3 个元素大于或等于 3 。

示例 4：

1
2
输入：nums = [3,6,7,7,0]
输出：-1

提示：

  • 1 <= nums.length <= 100
  • 0 <= nums[i] <= 1000

来源：力扣（LeetCode）

题解

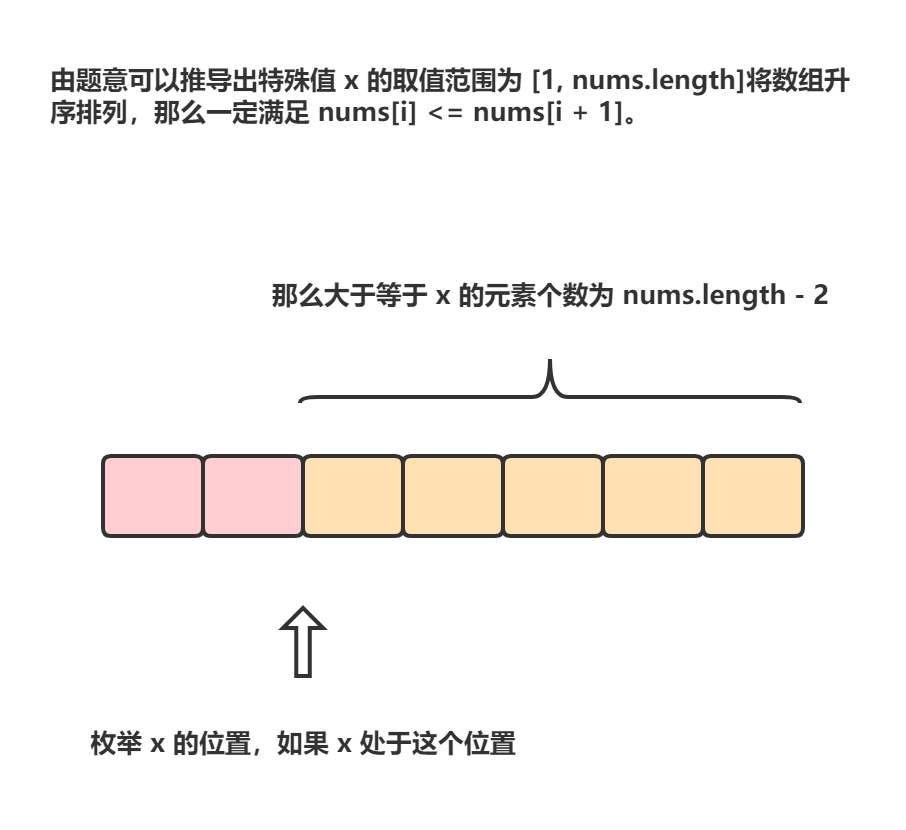
SpecialArrayWithXElementsGreaterThanOrEqualX

排序 + 一次遍历

1
2
3
4
5
6
7
8
9
10
11
12
public int specialArray(int[] nums) {
    Arrays.sort(nums);

    for (int i = 0; i < nums.length; i++) {
        int x = nums.length - i;
        if (nums[i] >= x && (i == 0 || x > nums[i - 1])) {
            return x;
        }
    }

    return -1;
}
  • 时间复杂度： O(nlogn)*，其中 *n 是数组 nums 的长度
  • 空间复杂度： *O(logn)*，即为排序需要的栈空间

submissions-2022091301

排序 + 枚举 + 二分查找

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
public int specialArray(int[] nums) {
    Arrays.sort(nums);

    // 枚举 x
    for (int i = 0; i < 1010; i++) {
        // 二分查找 x 在排序后数组中的位置
        int left = 0;
        int right = nums.length - 1;
        while (left < right) {
            int mid = left + (right - left >> 1);
            if (nums[mid] < i) left = mid + 1;
            else right = mid;
        }
        // 必须添加 nums[left] >= i 条件.
        // 举例 [0, 0] 当 x = 1 时, 二分查找比 1 大的数组元素的位置, 二分查找的结果 left = 1.
        // 因为没有更多更大的元素可以查找. 此时的结果是不满足 nums[left] > i 的情况的.
        if (nums[left] >= i && i == (nums.length - left)) return i;
    }

    return -1;
}
  • 时间复杂度： 排序的复杂度为 *O(nlogn)*；枚举找 x 的复杂度为 *O(Clogn)*，其中 C = 1e3 为 nums[i] 的值域大小
  • 空间复杂度： O(logn)

submissions-2022091302

排序 + 二分

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
public int specialArray(int[] nums) {
    // 只是将枚举过程优化了, 如果大于等于 x 的元素有 n 个且 n > x, 那么我们需要让 x 变大 n 变小, 从而寻找 x == n 的情况.
    Arrays.sort(nums);

    // 二分查找
    int left = 0;
    int right = 1010;
    while (left < right) {
        // 这里无论是哪种二分查找模板都没关系, 因为最终只要 count == mid 的情况
        int mid = left + (right - left >> 1);
        int count = this.countNums(nums, mid);
        if (count > mid){
            left = mid + 1;
        } else {
            right = mid;
        }
    }

    return this.countNums(nums, left) == left ? left : -1;
}

private int countNums(int[] nums, int x) {
    int left = 0;
    int right = nums.length - 1;
    while (left < right) {
        int mid = left + (right - left >> 1);
        if (nums[mid] < x) left = mid + 1;
        else right = mid;
    }
    if (nums[left] >= x) return nums.length - left;
    return 0;
}
  • 时间复杂度： 排序复杂度为 O(nlogn)*，二分查找复杂度为 *O(logC × logn)
  • 空间复杂度： O(logn)

submissions-2022091303

模拟（计数 + 枚举）

1
2
3
4
5
6
7
8
9
10
11
12
public int specialArray(int[] nums) {
    // 统计每个数字出现的次数
    int[] countArr = new int[1010];
    for (int num : nums) countArr[num]++;
    // 枚举 x
    for (int i = 1009, count = 0; i >=0 ; i--) {
        // 如果 nums[i] 大于 x, 那么 nums[i + 1] 也一定大于
        count += countArr[i];
        if (count == i) return i;
    }
    return -1;
}
  • 时间复杂度： O(nlogn)*，其中 *n 是数组 nums 的长度
  • 空间复杂度： O(C)

submissions-2022091304

参考资料

__END__