题目描述

给你二叉搜索树的根节点 root ，同时给定最小边界 low 和最大边界 high。通过修剪二叉搜索树，使得所有节点的值在 [low, high] 中。修剪树 不应该 改变保留在树中的元素的相对结构 (即，如果没有被移除，原有的父代子代关系都应当保留)。 可以证明，存在 唯一的答案 。

所以结果应当返回修剪好的二叉搜索树的新的根节点。注意，根节点可能会根据给定的边界发生改变。

示例 1：

1
2
输入：root = [1,0,2], low = 1, high = 2
输出：[1,null,2]

示例 2：

1
2
输入：root = [3,0,4,null,2,null,null,1], low = 1, high = 3
输出：[3,2,null,1]

提示：

  • 树中节点数在范围 [1, 10^4] 内
  • 0 <= Node.val <= 10^4
  • 树中每个节点的值都是 唯一 的
  • 题目数据保证输入是一棵有效的二叉搜索树
  • 0 <= low <= high <= 10^4

来源：力扣（LeetCode）

题解

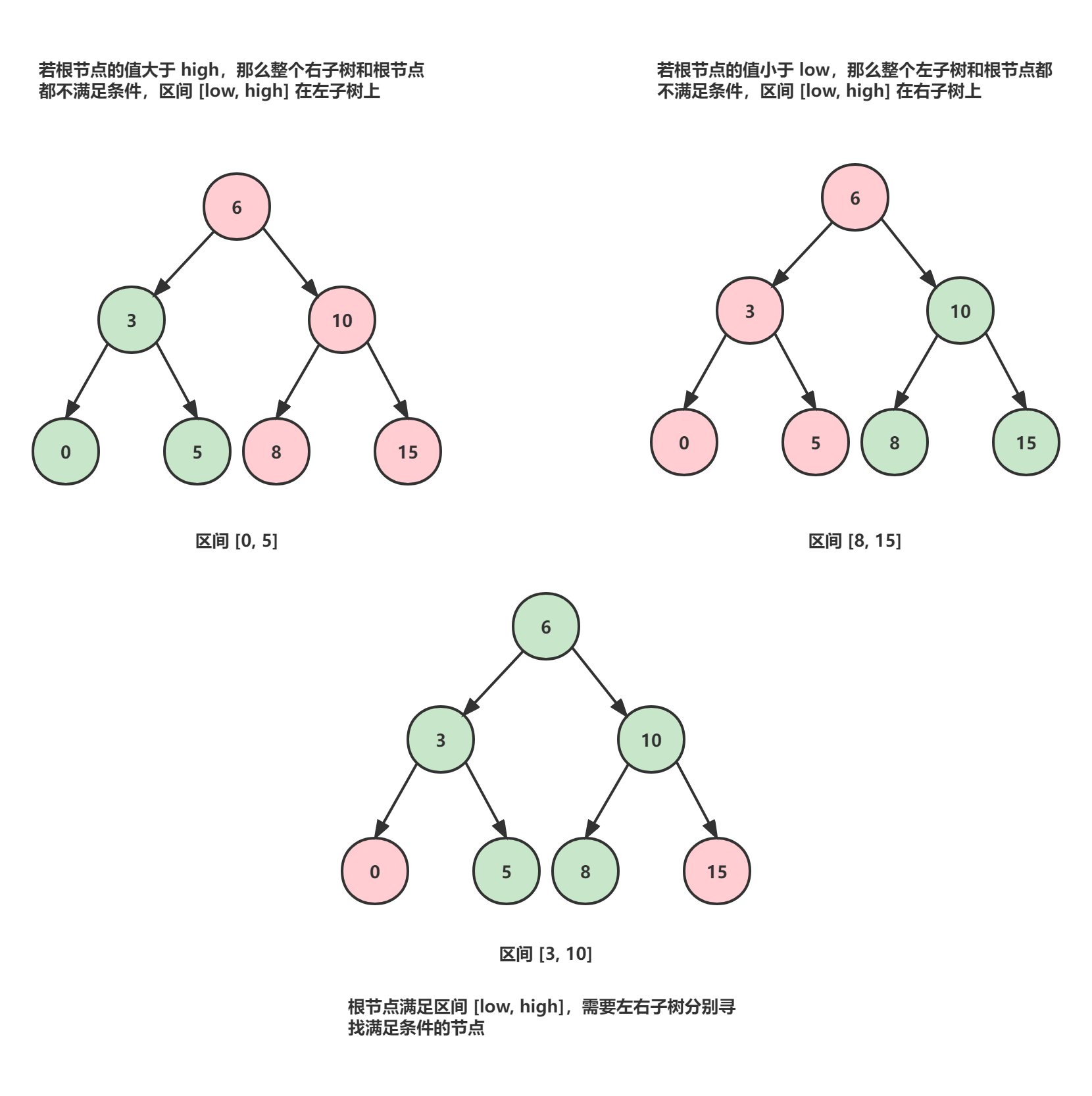
二叉查找树（Binary Search Tree），（又：二叉搜索树，二叉排序树）它或者是一棵空树，或者是具有下列性质的二叉树： 若它的左子树不空，则左子树上所有结点的值均小于它的根结点的值； 若它的右子树不空，则右子树上所有结点的值均大于它的根结点的值； 它的左、右子树也分别为二叉排序树。二叉搜索树作为一种经典的数据结构，它既有链表的快速插入与删除操作的特点，又有数组快速查找的优势。

TrimABinarySearchTree

迭代

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
public TreeNode trimBST(TreeNode root, int low, int high) {
    // 存储当前节点
    TreeNode current = root;
    // 最后一个满足条件的节点
    TreeNode prev = null;
    // 寻找左区间 low
    while (current != null) {
        // 寻找第一个 val < low 的节点
        while (current != null && current.val >= low) {
            prev = current;
            current = current.left;
        }
        // 如果因为 null 值结束, 则说明左边全部的节点都满足 val >= low
        if (current == null) break;
        // 如果当前节点 val < low, 那么它的左子树一定也不满足条件（左子树的值都比它的跟节点小）, 但是右子树可能满足条件, 所以将当前节点以及它的左子树剪除
        current = current.right;
        if (prev != null) prev.left = current;
        // 没有一个节点满足 val >= low, 则说明位于根节点以及左子树都不满足条件, 所以将根节点以及左子树剪除
        else root = current;
    }
    current = root;
    prev = null;
    // 寻找右区间 high
    while (current != null) {
        while (current != null && current.val <= high) {
            prev = current;
            current = current.right;
        }
        if (current == null) break;
        current = current.left;
        if (prev != null) prev.right = current;
        else root = current;
    }
    return root;
}
  • 时间复杂度： O(n)
  • 空间复杂度： O(1)

submissions-2022091001

迭代

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
public TreeNode trimBST(TreeNode root, int low, int high) {
    // 寻找第一个处于区间 [low, high] 的节点
    // 如果 root.val < low 证明区间 [low, high] 的节点在右子树中
    while (root != null && (root.val < low || root.val > high)) {
        root = (root.val < low) ? root.right : root.left;
    }
    // 如果重新寻找的节点为 null, 则证明没有满足条件的节点
    if (root == null) return null;
    // 此时, root 节点一定不为 null
    // 向左寻找区间
    for (TreeNode node = root; node.left != null; ) {
        if (node.left.val < low) node.left = node.left.right;
        else node = node.left;
    }
    // 向右寻找区间
    for (TreeNode node = root; node.right != null; ) {
        if (node.right.val > high) node.right = node.right.left;
        else node = node.right;
    }
    return root;
}
  • 时间复杂度： O(n)
  • 空间复杂度： O(1)

submissions-2022091002

递归

1
2
3
4
5
6
7
8
9
public TreeNode trimBST(TreeNode root, int low, int high) {
    if (root == null) return null;
    // 如果 root 的值小于 low, 证明符合条件的节点在 root 节点的右侧, 根节点 root 以及左子树不用考虑
    if (root.val < low) return trimBST(root.right, low, high);
    else if (root.val > high) return trimBST(root.left, low, high);
    root.left = trimBST(root.left, low, high);
    root.right = trimBST(root.right, low, high);
    return root;
}
  • 时间复杂度： O(n)
  • 空间复杂度： O(1)

submissions-2022091003

参考资料

__END__